
تاریخچه مسائل هزاره
اولین بار ۲۴ مه ۲۰۰۰، بهمنظور بزرگداشت ریاضیات در آغاز هزاره جدید، مؤسسه ریاضیات کِلی (CMI) در کمبریج، ماساچوست، 7 مسئله جایزهدار را تعیین کرد. این جوایز بهمنظور ثبت برخی از دشوارترین مسائلی که ریاضیدانان در آستانه هزاره دوم با آنها درگیر بودند، طراحی شد.
این 7 مسئله انتخاب شدند. درنهایت، هیئتمدیره CMI جایزه یکمیلیون دلاری را برای هرکدام از ۷ مسئله (درمجموع 7 میلیون دلار) تعریف کرد.
تمرکز این هیئت روی سؤالات کلاسیک مهمی است که سالها بدون راهحل باقی ماندهاند. هدف این کار علاوهبر جلب توجه عموم به این واقعیت که در ریاضیات هنوز مرزهای ناشناخته و مسائل حلنشده مهمی وجود دارد، تأکید بر اهمیت تلاش برای حل عمیقترین و دشوارترین مسائل و تقدیر از دستاوردهایی مهم در تاریخ ریاضیات است.
۷ مسئله با عنوان مسائل جایزه هزاره یا مسائل حلنشدنی مطرح شدند، شامل موارد زیر بودند:
- حدس پوانکاره
- فرضیه ریمان
- مسئله P در مقابل NP
- حدس بیرچ و سوینرتون-دایر
- حدس هاج
- معادله ناویر-استوکس
- نظریه یانگ-میلز
جالب این است که از این 7 مسئله لاینحل ریاضی، مسئله «حدس پوانکاره» حل شده است اما 6 مسئله دیگر همچنان حلنشده باقی ماندهاند. در ادامه، هریک از این مسائل را توضیح میدهیم.
حدس پوانکاره؛ مسئله حلشده

«هانری پوانکاره»
حدس پوانکاره یکی از سؤالات مشهور در ریاضیات است که سال 1904 ریاضیدان فرانسوی، «هانری پوانکاره» ، مطرح کرد. برای درک حدس پوانکاره ابتدا باید مفهوم «اتصال ساده» را بررسی کنیم. درصورتی که هر حلقهای را که روی فضایی سبهبعدی رسم کنیم، بتوانیم بدون پارهکردن یا برداشتن از سطح در نقطهای جمع کنیم، آن فضا فضای سهبعدی اتصال ساده دارد.
برای مثال، سطح یک دایره (کره دوبعدی) اتصال ساده دارد؛ چون هر حلقهای که روی آن بکشیم، میتوانیم آن را در نقطهای جمع کنیم اما دونات اینطور نیست؛ زیرا حلقههایی را که دور سوراخ آن کشیده میشوند، نمیتوان بدون پارهکردن، در یک نقطه جمع کرد.
پوانکاره میپرسد آیا این ویژگی اتصال ساده میتواند برای تعریف یکتایی منیفولدهای سهبعدی (فضای سهبعدی اقلیدسی) استفاده شود؟ به بیان سادهتر، آیا هر منیفولد سهبعدی که اتصال ساده دارد، کرهای سهبعدی است؟
حل مسئله حدس پوانکاره

«گریگوری پرلمان»
بین سالهای ۲۰۰۲ و ۲۰۰۳، «گریگوری پرلمان» ، ریاضیدان روس، ۳ مقاله در اینترنت منتشر کرد که شامل اثباتی مختصر برای حدس پوانکاره بود. اثبات پایهای او را چندین ریاضیدان توسعه داده شد و تا ۲۰۰۶ بهطور عمومی راهحلی معتبر شناخته شد.
پرلمان نشان داد هر منیفولد سهبعدی با استفاده از مجموعهای از قطعات استاندارد با یکی از 8 هندسه ممکن ساخته میشود. (این 8 نوع هندسه شامل ساختارهای خاصی مثل فضاهای کروی، هذلولی، اقلیدسی و هندسههای دیگر است که هرکدام خصوصیات ریاضی متفاوتی دارند.) به بیان سادهتر، هر فضای سهبعدی پیچیده را میتوان به قطعاتی سادهتر و با ساختارهای مشخص تقسیم کرد.
راهحل پرلمان یکی از دستاوردهای بزرگ ریاضیاتی قرن بیستم شناخته میشود. سال 2006، مدال فیلدز بهخاطر این دستاورد به او اعطا شد که البته آن را نپذیرفت. همچنین سال ۲۰۱۰، CMI جایزه مسئله هزاره را برای اثبات حدس پوانکاره به پرلمان پیشنهاد داد اما او این جایزه را نیز نپذیرفت.
فرضیه ریمان ، در میان مسائل غیرقابل حل ریاضی

«گئورگ فردریش برنهارد ریمان»
فرضیه ریمان را «گئورگ فردریش برنهارد ریمان» ، ریاضیدان آلمانی، سال ۱۸۵۹ مطرح کرد. این فرضیه به چگونگی توزیع اعداد اول در مجموعه اعداد طبیعی مرتبط است. اعداد اول اعدادی هستند که فقط بر یک و خودشان بخشپذیرند و باوجود نقش مهمشان، نظم خاصی در پراکندگیشان وجود ندارد.
ریمان دریافت توزیع اعداد اول میتواند به تابعی ریاضی به نام «تابع زتای ریمان» مرتبط باشد. تابع زتای ریمان بهصورت زیر تعریف میشود که در آن s عددی مختلط است. این تابع برای مقادیر مختلفی از s مقدار میگیرد و زمانی که این مقدار به صفر برسد، ریشهای برای تابع به دست میآید.
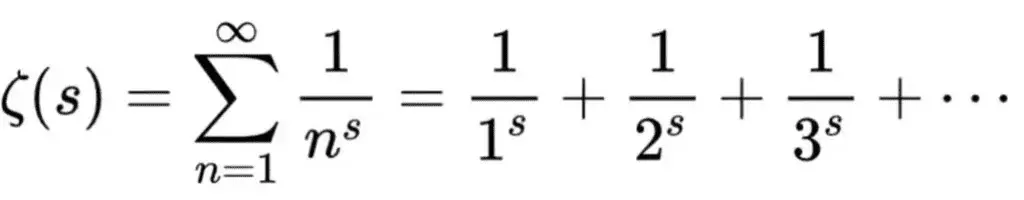
فرضیه ریمان بیان میکند تمامی ریشههای معادله